🧠 Crack Google Interview: Can you finding the median of two sorted arrays?

Google LeetCode

Imagine you have two sorted lists of numbers and you want to find the median when they are combined. The median is the "middle" value – if the total number of elements is odd, it's the middle element, and if it's even, the median is the average of the two middle elements¹. For example, consider these cases:

• Example 1: nums1 = [1, 3], nums2 = [2] – When combined, the sorted array is [1, 2, 3] and the median is 2.0.

• Example 2: nums1 = [1, 2], nums2 = [3, 4] – The combined sorted array is [1, 2, 3, 4]. The two middle elements are 2 and 3, so the median is (2 + 3) / 2 = 2.5.

Finding the median by actually merging the arrays is straightforward. However, the challenge (and the typical interview twist) is to do this efficiently without necessarily merging everything. In fact, the known problem expects an algorithm with time complexity on the order of O(log(min(m, n)))², which is much faster than a full merge. Let's start simple and build up to that optimal solution.

Approach 1: Merge and find the median

The most intuitive solution is: merge the two sorted arrays and then pick out the median. This is similar to the merge step in merge sort. Because the arrays are already sorted, we can do this in linear time by iterating through both lists:

• Idea: Walk through both arrays with two pointers, always taking the smaller current element into a merged result. This way, we build the sorted combined list without needing an extra sort step³.

• Stop early (optional): We actually don’t need to merge all elements – we can stop once we reach the median position. For instance, if the total length is N = m + n, we only need to process the first N/2 + 1 elements to determine the median. But for simplicity, we'll illustrate by merging fully, then finding the median.

• Complexity: Merging two sorted arrays this way takes O(m + n) time (linear in the total number of elements). If we create a new merged array, it uses O(m + n) extra space. We can reduce space to O(1) by tracking only a few values as we merge, but using a new array is conceptually easier for beginners.

Step-by-step example (merge approach): Suppose nums1 = [1, 3] and nums2 = [2]. We’ll merge them step by step:

1. Start with two pointers i = 0 (at nums1[0] = 1) and j = 0 (at nums2[0] = 2). Compare 1 and 2. The smaller value is 1, so append 1 to the merged list.

2. Increment i (now i = 1, pointing to nums1[1] = 3), and compare nums1[1] = 3 with nums2[0] = 2. Now 2 is smaller, so append 2 to the merged list and increment j.

3. Pointer j moves to 1, which is beyond the end of nums2 (since nums2 had only one element). This means all remaining elements are in nums1. Append the leftover 3 from nums1 to the merged list.

4. The merged array is now [1, 2, 3]. With 3 elements (odd length), the median is the middle element 2.0.

We get the correct result as expected. If the total number of elements were even, we would take the average of the two middle values. For example, merging [1, 2] and [3, 4] gives [1, 2, 3, 4] and the median is (2 + 3) / 2 = 2.5.

Implementation of merge method

Let's implement this merging approach in C++ first.

C++

We will merge the arrays using two indices and then compute the median. For clarity, we'll merge completely into a new array (which is easy to understand). Comments are added to explain each part of the process.

#include <iostream>
#include <vector>
using namespace std;

double findMedianMerged(const vector<int>& nums1, const vector<int>& nums2) {
    int m = nums1.size();
    int n = nums2.size();
    // Pointers for nums1 and nums2
    int i = 0, j = 0;
    vector<int> merged;
    merged.reserve(m + n);  // allocate merged array capacity in advance

    // Merge the two sorted arrays
    while(i < m && j < n) {
        if(nums1[i] < nums2[j]) {
            merged.push_back(nums1[i]);
            i++;
        } else {
            merged.push_back(nums2[j]);
            j++;
        }
    }
    // If any elements remain in nums1 or nums2, append them
    while(i < m) {
        merged.push_back(nums1[i]);
        i++;
    }
    while(j < n) {
        merged.push_back(nums2[j]);
        j++;
    }

    // Now merged contains all elements in sorted order.
    int total = m + n;
    if(total % 2 == 1) {
        // If odd number of elements, return the middle one
        return merged[total/2];
    } else {
        // If even, return average of the two middle elements
        int mid = total / 2;
        double median = (merged[mid - 1] + merged[mid]) / 2.0;
        return median;
    }
}

int main() {
    vector<int> nums1 = {1, 3};
    vector<int> nums2 = {2};
    cout << "Median is: " << findMedianMerged(nums1, nums2) << endl;
    // You can test with other examples:
    // nums1 = {1, 2}, nums2 = {3, 4} should output 2.5
    return 0;
}

Output (for the example inputs):

Median is: 2

Note: The output 2 corresponds to 2.0 as a double – we could format it, but the value is correct.

Python

Now let's do the same in Python. Python offers convenient list operations, but we'll stick to the logical two-pointer approach for clarity.

def find_median_merged(nums1, nums2):
    i, j = 0, 0
    merged = []
    # Merge until one list is exhausted
    while i < len(nums1) and j < len(nums2):
        if nums1[i] < nums2[j]:
            merged.append(nums1[i])
            i += 1
        else:
            merged.append(nums2[j])
            j += 1
    # Append any remaining elements
    merged.extend(nums1[i:])
    merged.extend(nums2[j:])
    # Calculate median
    total = len(merged)
    if total % 2 == 1:
        return float(merged[total // 2])        # middle element for odd length
    else:
        mid = total // 2
        return (merged[mid - 1] + merged[mid]) / 2.0  # average of two middle for even length

# Example usage:
print(find_median_merged([1, 3], [2]))       # Output: 2.0
print(find_median_merged([1, 2], [3, 4]))   # Output: 2.5

The function find_median_merged will merge the two lists and compute the median. We convert the result to float for the odd case to be explicit about the decimal (in Python, dividing by 2.0 ensures the result is float as well).

Rust

Finally, let's implement the merge approach in Rust. We will use indices to traverse both arrays (slices) and build a merged vector. Rust doesn’t have built-in growable arrays like Python, but we can use a Vec for the merged result.

fn find_median_merged(nums1: &[i32], nums2: &[i32]) -> f64 {
    let m = nums1.len();
    let n = nums2.len();
    let mut merged: Vec<i32> = Vec::with_capacity(m + n);
    let (mut i, mut j) = (0, 0);
    // Merge the two sorted arrays into merged
    while i < m && j < n {
        if nums1[i] < nums2[j] {
            merged.push(nums1[i]);
            i += 1;
        } else {
            merged.push(nums2[j]);
            j += 1;
        }
    }
    // Append leftovers from either array
    if i < m {
        merged.extend(&nums1[i..]);
    }
    if j < n {
        merged.extend(&nums2[j..]);
    }
    // Calculate median
    let total = merged.len();
    if total % 2 == 1 {
        merged[total / 2] as f64
    } else {
        let mid = total / 2;
        (merged[mid - 1] as f64 + merged[mid] as f64) / 2.0
    }
}

fn main() {
    let nums1 = vec![1, 3];
    let nums2 = vec![2];
    println!("Median is: {}", find_median_merged(&nums1, &nums2));
    // Try other examples:
    // nums1 = [1, 2], nums2 = [3, 4] -> should print 2.5
}

Here we return the median as an f64 (floating-point number) for generality. The approach is identical: iterate with two indices, push the smaller element, and then handle any remaining elements.

Time and space complexity (merge approach)

• Time Complexity: Merging takes linear time, i.e. O(m + n) steps in the worst case, where m and n are the lengths of the two arrays. This is efficient for moderate sizes, but if m and n are very large (millions of elements), it will iterate over every element.

• Space Complexity: In our implementation, we used an extra array of size m+n to store the merged result (so, O(m + n) space). This can be improved: we could compute the median on the fly without storing all elements by keeping track of the middle values as we merge. In that optimized version, the extra space would be only a few variables (constant space O(1)). We chose the clearer approach of actually merging to make it easier to follow.

The merge method is straightforward and beginner-friendly, but it isn't optimal if efficiency is a concern. Next, let's explore the clever binary search method that finds the median without fully merging the arrays, achieving the required O(log(min(m, n))) time complexity.

Approach 2: Binary search partition (optimal solution)

To find the median faster, we need a different insight. Think about the combined sorted array conceptually: if you could split this merged array into two halves of equal length (or as equal as possible when the total is odd), the median would lie around that split point. In fact, if we split the merged array into a left half and a right half of equal size, then all elements in the left half are less than or equal to all elements in the right half, and the median is the boundary between them⁴. For an even total number of elements, the median is the average of the two boundary values (max of left half and min of right half); for an odd total, the median is the boundary element that falls in the larger half.

The trick is: we don't actually have the merged array explicitly. But we can simulate this "partitioning" by cutting the two arrays at certain points. We choose an index i in the first array and an index j in the second array such that the left side of nums1 up to i and the left side of nums2 up to j together form the left half of the merged order. In other words, i + j = (m + n + 1) / 2 (this formula gives the size of the left half). Then the remaining elements of nums1 and nums2 form the right half.

Now we need to find the perfect partition where every element on the left half is <= every element on the right half. At that partition:

• Let L1 be the element just to the left of the cut in nums1 (the last element of the left part of nums1), and R1 be the element just to the right of the cut in nums1 (the first element of the right part of nums1). Similarly, define L2 and R2 for nums2.

• We want L1 <= R2 and L2 <= R1 to ensure that all left-half elements are smaller than all right-half elements. If this condition is met, the partition is correct.

• If L1 > R2, it means we cut nums1 too far to the right (we have an element in nums1's left part that is greater than something in nums2's right part). So we should move the cut in nums1 to the left (take fewer elements from nums1).

• If L2 > R1, it means we haven't taken enough elements from nums1 (the cut in nums1 is too far left), so we need to move it to the right to include more from nums1.

This is a perfect scenario for binary search: we can adjust the index i in nums1 based on comparisons, halving the search space each time. We always binary-search on the smaller array to minimize the search range and to ensure j = half - i stays within the bounds of the larger array.

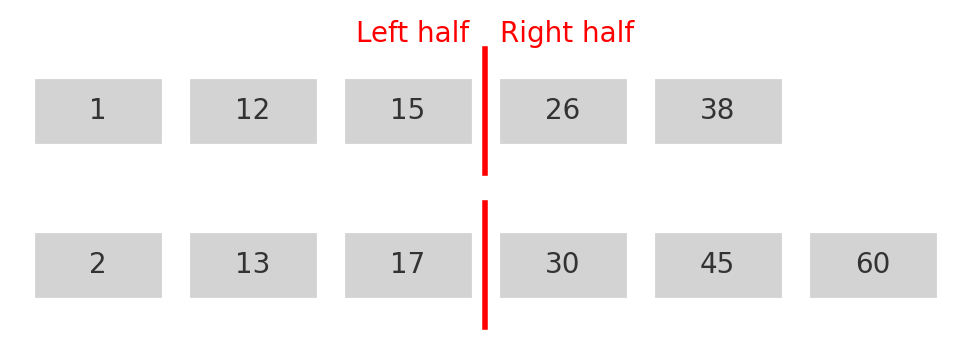
Illustration of an optimal partition between two arrays. The red line represents a cut that splits the combined elements into a left half and right half. Here, nums1 (top) is cut at index 3 and nums2 (bottom) is cut at index 3, creating two left subarrays of equal total length (6 elements on the left side out of 11). All elements on the left side are ≤ all elements on the right side, so this partition is valid for median calculation.

In the image above, for example, L1 = 15 (last element of nums1's left side), R1 = 26 (first element of nums1's right side), L2 = 17 (last of nums2's left side), and R2 = 30 (first of nums2's right side). We can verify L1 <= R2 (15 ≤ 30) and L2 <= R1 (17 ≤ 26), so the condition holds. Since the total number of elements is 11 (odd), the median is the larger of L1 and L2, which is 17. (If it were even, we would take the average of max(L1,L2) and min(R1,R2)).

Steps for the binary search approach

Let's break down the algorithm in simple steps:

1. Ensure one array is smaller: If not, swap them. Let A be the smaller array of length m, and B be the larger array of length n. This way, we binary search on A (fewer possibilities to check).

2. Set up binary search on A: Initialize low = 0 and high = m (meaning the cut in A can range from 0 to all elements of A).

3. Binary search loop: While low <= high:

   • Calculate i = (low + high) // 2 (the tentative cut position in A). Then compute j = (m + n + 1) / 2 - i (the cut position in B such that left half has the required number of elements).

   • Determine L1, R1, L2, R2:

     • L1 = A[i-1] if i > 0, otherwise -∞ (a conceptual negative infinity if i = 0, meaning nothing from Aon the left side).

     • R1 = A[i] if i < m, otherwise +∞ (if i = m, it means all of A is on the left side and nothing on the right).

     • L2 = B[j-1] if j > 0, otherwise -∞.

     • R2 = B[j] if j < n, otherwise +∞.

   • Check partition validity:

     • If L1 <= R2 and L2 <= R1, we found the correct partition. Proceed to compute the median:

       • If (m+n) is odd, the median is max(L1, L2) (the larger of the two left-part ends).

       • If (m+n) is even, the median is the average of max(L1, L2) and min(R1, R2).

     • If L1 > R2, we are too far right in A (an element from A's left side is too big), so move left: set high = i - 1.

     • Else if L2 > R1, we are too far left in A (an element from B's left side is too big), so move right: set low = i + 1.

4. Eventually the binary search will find the correct partition (the problem guarantees a solution exists). The median is then computed as above.

This approach might sound complex at first, but it’s very efficient. We are essentially doing a binary search on the index i, which has at most m+1 possible values (where m is the smaller array length). So the time complexity is O(log m) which is O(log(min(m, n))).

Implementation of binary search method

Next, let's look at code for this method in C++, Python, and Rust.

C++

We'll implement the above logic step by step. To handle the "negative infinity" and "positive infinity" for out-of-bound indices, we can use sentinel values like INT_MIN and INT_MAX from <limits.h>. These act as -∞ and +∞ for comparison purposes (since all real array values will be within normal integer range):

#include <iostream>
#include <vector>
#include <limits.h>
using namespace std;

double findMedianBinary(const vector<int>& nums1, const vector<int>& nums2) {
    int m = nums1.size();
    int n = nums2.size();
    // Ensure nums1 is the smaller array
    if(m > n) {
        return findMedianBinary(nums2, nums1);
    }

    int low = 0, high = m;
    int half_len = (m + n + 1) / 2;  // half length (rounded up)
    while(low <= high) {
        int i = (low + high) / 2;    // try cutting at i in nums1
        int j = half_len - i;        // remaining elements from nums2

        // Compute L1, R1, L2, R2 with out-of-bound checks
        int L1 = (i == 0) ? INT_MIN : nums1[i - 1];
        int R1 = (i == m) ? INT_MAX : nums1[i];
        int L2 = (j == 0) ? INT_MIN : nums2[j - 1];
        int R2 = (j == n) ? INT_MAX : nums2[j];

        // Check if partition is valid
        if(L1 <= R2 && L2 <= R1) {
            // Found the correct partition
            if((m + n) % 2 == 1) {
                // If total length is odd, median is max of left parts
                return max(L1, L2);
            } else {
                // If even, median is average of max(L1, L2) and min(R1, R2)
                int left_max = max(L1, L2);
                int right_min = min(R1, R2);
                return (left_max + (long long)right_min) / 2.0;
            }
        }
        else if(L1 > R2) {
            // We are too far right in nums1, go left
            high = i - 1;
        }
        else {
            // We are too far left in nums1, go right
            low = i + 1;
        }
    }
    // If we reach here, input was not valid (arrays not sorted or something)
    return 0.0;
}

int main() {
    vector<int> nums1 = {1, 3};
    vector<int> nums2 = {2};
    cout << "Median is: " << findMedianBinary(nums1, nums2) << endl;
    // Test with the second example:
    nums1 = {1, 2};
    nums2 = {3, 4};
    cout << "Median is: " << findMedianBinary(nums1, nums2) << endl;
    return 0;
}

Let's briefly verify the outputs:

Median is: 2
Median is: 2.5

This matches the expected medians for the test examples.

Python

Now the same idea in Python. We will use float('inf') as our positive infinity and -float('inf') for negative infinity to handle edge cases cleanly:

def find_median_binary(nums1, nums2):
    # Ensure nums1 is the smaller array
    if len(nums1) > len(nums2):
        return find_median_binary(nums2, nums1)
    m, n = len(nums1), len(nums2)
    low, high = 0, m
    half_len = (m + n + 1) // 2  # half length (rounded up)
    while low <= high:
        i = (low + high) // 2
        j = half_len - i
        # Boundaries or sentinel values for L1, R1, L2, R2
        L1 = -float('inf') if i == 0 else nums1[i-1]
        R1 = float('inf')  if i == m else nums1[i]
        L2 = -float('inf') if j == 0 else nums2[j-1]
        R2 = float('inf')  if j == n else nums2[j]
        # Check if we found the correct partition
        if L1 <= R2 and L2 <= R1:
            if (m + n) % 2 == 1:
                return max(L1, L2) * 1.0  # ensure float
            else:
                return (max(L1, L2) + min(R1, R2)) / 2.0
        elif L1 > R2:
            # move partition in nums1 to the left
            high = i - 1
        else:
            # move partition in nums1 to the right
            low = i + 1

# Testing the function with the examples:
print(find_median_binary([1, 3], [2]))    # 2.0
print(find_median_binary([1, 2], [3, 4]))  # 2.5

The logic is the same as in C++: we binary search on the smaller array and adjust the partition based on the comparisons. The outputs should confirm it works correctly.

Rust

Finally, let's implement the optimal approach in Rust. We will carefully handle indices and use i32::MIN and i32::MAXfrom Rust's standard library as sentinel values for -∞ and +∞:

fn find_median_binary(nums1: &[i32], nums2: &[i32]) -> f64 {
    // Ensure nums1 is smaller
    let (mut a, mut b) = (nums1, nums2);
    if a.len() > b.len() {
        // swap a and b if necessary
        a = nums2;
        b = nums1;
    }
    let m = a.len();
    let n = b.len();
    let half_len = (m + n + 1) / 2;
    let mut low = 0;
    let mut high = m;
    use std::cmp::{max, min};
    use std::i32;
    while low <= high {
        let i = (low + high) / 2;
        let j = half_len - i;
        // Use sentinel values for boundaries
        let L1 = if i == 0 { i32::MIN } else { a[i-1] };
        let R1 = if i == m { i32::MAX } else { a[i] };
        let L2 = if j == 0 { i32::MIN } else { b[j-1] };
        let R2 = if j == n { i32::MAX } else { b[j] };
        if L1 <= R2 && L2 <= R1 {
            // Correct partition found
            if (m + n) % 2 == 1 {
                return max(L1, L2) as f64;
            } else {
                let left_max = max(L1, L2) as f64;
                let right_min = min(R1, R2) as f64;
                return (left_max + right_min) / 2.0;
            }
        } else if L1 > R2 {
            high = i - 1;
        } else {
            low = i + 1;
        }
    }
    // This return would only happen if input arrays were not sorted as assumed
    0.0
}

fn main() {
    let nums1 = vec![1, 3];
    let nums2 = vec![2];
    println!("Median is: {}", find_median_binary(&nums1, &nums2));
    let nums3 = vec![1, 2];
    let nums4 = vec![3, 4];
    println!("Median is: {}", find_median_binary(&nums3, &nums4));
}

In this Rust code, we use i32::MIN and i32::MAX as stand-ins for negative and positive infinity (assuming the array elements themselves don’t reach these extreme values). The code follows the same binary search procedure. The output will be:

Median is: 2
Median is: 2.5

for the example tests, as expected.

Time and space complexity (binary search approach)

• Time Complexity: This algorithm runs in O(log(min(m, n))) time because we binary search on the smaller array. For example, if one array has 1000 elements and the other has 1,000,000 elements, we effectively do roughly log2(1000) iterations, which is very fast (around 10 steps). This is a significant improvement over the O(m+n) linear merge when dealing with large data sizes.

• Space Complexity: Only a constant amount of extra space is used (O(1)), since we are just using a few variables for indices and boundary values. We do not create any large additional data structures.

Conclusion

Finding the median of two sorted arrays is a classic problem that teaches several valuable lessons. We started with a simple merging approach that is easy to understand but scans through all elements. Then we explored an optimal solution using binary search and array partitioning, which is trickier but much more efficient. Key takeaways include understanding the median in terms of partitioning two halves of a sorted sequence, and how leveraging binary search can drastically reduce time complexity by narrowing down the search space.

This problem is a great example of how a divide-and-conquer strategy (binary search) can outperform a brute-force approach. If you found this interesting, you might also want to explore related problems, such as finding the k-th smallest element of two sorted arrays or the "Median of K Sorted Arrays" generalization.

Keep practicing and experimenting with these ideas – with each problem, you'll strengthen your understanding of algorithms and problem-solving techniques.

Happy coding!

1. Median of Two Sorted Arrays

2. LeetCode Q4: Median of Two Sorted Arrays

3. Median of two Sorted Arrays of Different Sizes

4. How to find the median between two sorted arrays?